Saulo Martiello Mastelini (mastelini@usp.br) Outras redes: Github - Linkedin
MBA em Ciência de Dados Universidade de São Paulo, São Carlos, Brasil Copyright (c) 2020
Disclaimer: Eu gerei um arquivo de markdown para essa postagem. Nesse notebook eu utilizo plots interativos para melhor entender o funcionamento dos algoritmos. Sugiro fazer o download do notebook original aqui e o executar localmente 😄
import time
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
Plano
Nessa prática abordaremos basicamente dois algoritmos para clustering particional, que se baseiam em diferentes estratégias:
- Protótipo
- k-Means
- k-Medians
- Partitioning Around Medoids (PAM) ou k-Medoids
- Densidade 3. DBSCAN
Lembrete:
Apesar de alguns algoritmos de agrupamento oferecerem uma função predict, estamos falando de um paradigma descritivo de aprendizado, como apresentado em aula. É importante sempre nos lembrarmos das diferenças desse tipo de atividade em relação à tarefas de predição (aprendizado supervisionado).
1. Clustering Particional: protótipos
1.1. k-Means
O k-Means busca separar os dados em grupos de igual variância. Para tal, o k-Means minimiza um critério conhecido como Inertia (inércia) ou Within-cluster sum-of-squares. É o equivalente a miminizar a distância euclidiana ao quadrado de cada ponto para o seu centróide ou, ainda, a variância intra-cluster (leitura interessante). A inércia mede quão coerentes os clusters são internamente. No entanto, temos alguns problemas com essa abordagem:
- A inércia assume que os clusters são convexos e isotrópicos (seus raios são iguais), o que nem sempre é verdade.
- A inércia não é uma métrica com range bem definido: apenas sabemos que quanto menor, melhor e, que zero é o valor mínimo possível. Em espaços com muitas dimensões, o uso da distância euclidiana pode nos levar a problemas devido à um caso específico da tão dita maldição da dimensionalidade. Nesse caso, vale a pena utilizar um algoritmo para redução de dimensões, como a Análise de Componentes Principais (PCA), antes do k-Means (de bônus, reduzimos o tempo de computação).
Começarei definindo uma implementação simples desse algoritmo e depois avaliaremos o passo-a-passo de sua implementação.
class KMeans:
def __init__(self, k, etol=1e-3, max_iter=100, random_state=42):
self.k = k
self.etol = etol
self.max_iter = max_iter
self.random_state = random_state
# Define semente de geração aleatória
np.random.seed(self.random_state)
# Variáveis internas
self.cluster_centers_ = None
self.n_iter_ = 0 # Número de iterações
def _clustering_criterion(self, X, cluster_center):
# Within cluster sum-of-squares
return np.sum((X - cluster_center) ** 2, axis=1)
def _pick_centers(self, X, verbose=False):
# Vou selecionar aleatoriamente k linhas dos meus dados para serem
# os centros iniciais
sel_rows = np.random.choice(X.shape[0], size=self.k, replace=False)
if verbose:
print('\nLinhas selecionadas como centros dos clusters:', sel_rows)
self.cluster_centers_ = np.zeros((self.k, X.shape[1]))
# Note que o "label" que cada centro recebe depende na seleção inicial
# (não existe uma noção de ordem aqui)
for cluster_id, row in enumerate(sel_rows):
self.cluster_centers_[cluster_id] = X[row]
if verbose:
print('Centros selecionados:')
for center_id, center in enumerate(self.cluster_centers_):
print(f'{center_id}: {center}')
def _update_centers(self, X, verbose=False):
scores = self.predict(X)
new_centers = np.zeros_like(self.cluster_centers_)
for center_id in range(self.k):
new_centers[center_id] = np.mean(X[scores == center_id], axis=0)
if verbose:
print('\nMudança dos centros:')
for center_id in range(self.k):
print(f'{center_id}: {self.cluster_centers_[center_id]} -> {new_centers[center_id]}')
return new_centers
def _stop_criteria_convergence(self, new_centers, verbose=False):
diff = np.sum((self.cluster_centers_ - new_centers) ** 2)
check = diff < self.etol
if verbose:
print(f'Variação dos centros: {diff}')
if check:
print(f'\nVariação dos centros é menor que "etol": {diff}. Parando.')
return check
def _stop_criteria_max_iter(self, verbose=False):
check = self.n_iter_ >= self.max_iter
if verbose:
print(f'Iteração {self.n_iter_}')
if check:
print(f'\nNúmero máximo de iterações atingido: {self.n_iter_}. Parando.')
return check
def fit(self, X, verbose=False, cycle_callback=None):
# Inicializa os centros
self._pick_centers(X, verbose=verbose)
p_out = None
while True: # Loop infinito. Os critérios de parada definirão o fim dos ciclos
new_centers = self._update_centers(X, verbose=verbose)
# Pequeno acochambramento
if cycle_callback is not None:
p_out = cycle_callback(X, self.predict(X), new_centers, fig=p_out)
if self._stop_criteria_convergence(new_centers, verbose=verbose):
break
self.cluster_centers_ = new_centers
# Pequeno acochambramento
if cycle_callback is not None:
p_out = cycle_callback(X, self.predict(X), self.cluster_centers_, fig=p_out)
# Atualiza o número de iterações
self.n_iter_ += 1
if self._stop_criteria_max_iter(verbose=verbose):
break
return self
def predict(self, X, verbose=False):
# Matriz com n_instances x n_clusters
errors = np.zeros((X.shape[0], self.k))
for center_id, center in enumerate(self.cluster_centers_):
errors[:, center_id] = self._clustering_criterion(X, center)
if verbose:
print(errors)
return np.argmin(errors, axis=1)
Agora vamos aos poucos entender o papel de cada parte
1.1.1. A iniciar pela seleção dos centros
# Vou gerar uma matriz de numeros aleatórios
np.random.seed(7)
X_toy = np.random.uniform(size=(20, 2))
print('Dados:')
print(X_toy)
kmeans = KMeans(k=3)
kmeans._pick_centers(X_toy, verbose=True)
Dados:
[[0.07630829 0.77991879]
[0.43840923 0.72346518]
[0.97798951 0.53849587]
[0.50112046 0.07205113]
[0.26843898 0.4998825 ]
[0.67923 0.80373904]
[0.38094113 0.06593635]
[0.2881456 0.90959353]
[0.21338535 0.45212396]
[0.93120602 0.02489923]
[0.60054892 0.9501295 ]
[0.23030288 0.54848992]
[0.90912837 0.13316945]
[0.52341258 0.75040986]
[0.66901324 0.46775286]
[0.20484909 0.49076589]
[0.37238469 0.47740115]
[0.36589039 0.83791799]
[0.76864751 0.31399468]
[0.57262533 0.27604905]]
Linhas selecionadas como centros dos clusters: [ 0 17 15]
Centros selecionados:
0: [0.07630829 0.77991879]
1: [0.36589039 0.83791799]
2: [0.20484909 0.49076589]
Como sempre, vou definir uma função simples de plot para não ficar repetindo código sem necessidade
def plot_cluster(X, labels=None, centers=None, fig=None):
# Figura começando do zero
if fig is None:
dims = (3, 3) # Sem legenda
if labels is not None:
if centers is None:
dims = (4, 3) # Sem centros
else:
dims = (5, 3) # Com centros
fig, ax = plt.subplots(figsize=dims)
else: # Reciclando figura anterior
ax = fig.axes[0]
if labels is None:
ax.scatter(X[:, 0], X[:, 1])
else:
for center in np.unique(labels):
imask = labels == center
ax.scatter(X[imask, 0], X[imask, 1], label=center)
if centers is not None:
ax.scatter(centers[:, 0], centers[:, 1], marker='+', c='black',
label='center', s=200)
ax.legend(loc='upper left', bbox_to_anchor=(1.05, 1))
plt.tight_layout()
plt.close()
return fig
plot_cluster(X_toy)
1.1.2. Função predict
Notem que a as linhas escolhidas como centros iniciais tem inércia zero.
scores = kmeans.predict(X_toy, verbose=True)
print('\nScores:', scores)
[[0. 0.0872217 0.10013214]
[0.1343041 0.01835843 0.1086993 ]
[0.87131405 0.46431895 0.60002426]
[0.68154201 0.60483922 0.26309877]
[0.11533453 0.12376477 0.00412679]
[0.36408199 0.09934991 0.32298943]
[0.6025721 0.59618219 0.21148855]
[0.06169058 0.01118163 0.1823549 ]
[0.12623957 0.17209482 0.00156607]
[1.30090467 0.98058128 0.74462614]
[0.30379992 0.06765605 0.36759328]
[0.07727366 0.10215258 0.00397996]
[1.11187401 0.79177803 0.62388453]
[0.20077302 0.03247092 0.16889769]
[0.44874673 0.22890569 0.21597796]
[0.10013214 0.14644888 0. ]
[0.17917816 0.13001457 0.02824679]
[0.0872217 0. 0.14644888]
[0.69641887 0.43670894 0.34911672]
[0.50021533 0.35843605 0.18136269]]
Scores: [0 1 1 2 2 1 2 1 2 2 1 2 2 1 2 2 2 1 2 2]
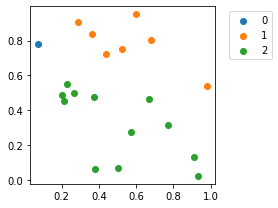
Sem visualizar os centroides
plot_cluster(X_toy, scores)
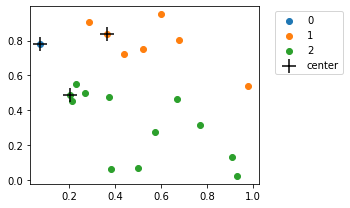
Com os centroides
plot_cluster(X_toy, scores, kmeans.cluster_centers_)
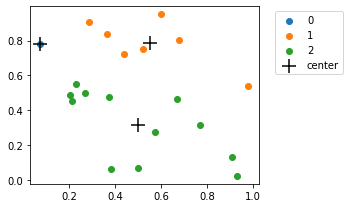
1.1.3. Por fim, vamos testar a função que atualiza os centroides
new_centroids = kmeans._update_centers(X_toy, verbose=True)
Mudança dos centros:
0: [0.07630829 0.77991879] -> [0.07630829 0.77991879]
1: [0.36589039 0.83791799] -> [0.55337517 0.78767871]
2: [0.20484909 0.49076589] -> [0.50183692 0.31854301]
plot_cluster(X_toy, scores, new_centroids)
# Vou forçar a troca dos centroides
kmeans.cluster_centers_ = new_centroids
scores = kmeans.predict(X_toy)
print('\nScores:', scores)
Scores: [0 1 1 2 2 1 2 0 2 2 1 0 2 1 2 0 2 1 2 2]
plot_cluster(X_toy, scores, kmeans.cluster_centers_)
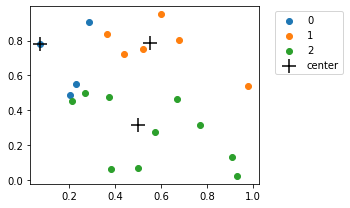
1.1.4. Vamos avaliar nossos critérios de parada
kmeans.n_iter_ += 1
# Iterações (iteramos apenas uma vez)
kmeans._stop_criteria_max_iter(verbose=True)
Iteração 1
False
Let’s try again: mais uma iteração
new_centroids = kmeans._update_centers(X_toy, verbose=True)
Mudança dos centros:
0: [0.07630829 0.77991879] -> [0.19990146 0.68219203]
1: [0.55337517 0.78767871] -> [0.5975801 0.76735957]
2: [0.50183692 0.31854301] -> [0.55868911 0.27832604]
kmeans.n_iter_ += 1
# Iterações (iteramos duas vezes)
kmeans._stop_criteria_max_iter(verbose=True)
Iteração 2
False
# Convergência
kmeans._stop_criteria_convergence(new_centroids, verbose=True)
Variação dos centros: 0.03204231220845901
False
# Vou atualizar mais uma vez os centroides de forma manual
kmeans.cluster_centers_ = new_centroids
scores = kmeans.predict(X_toy)
print('\nScores:', scores)
Scores: [0 1 1 2 0 1 2 0 0 2 1 0 2 1 2 0 0 0 2 2]
plot_cluster(X_toy, scores, kmeans.cluster_centers_)
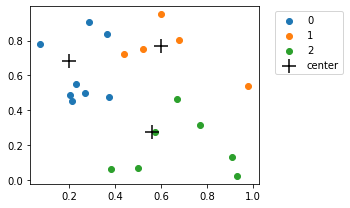
E assim por diante…
E se mudarmos a inicialização?
kmeans = KMeans(k=3, random_state=0)
kmeans._pick_centers(X_toy, verbose=True)
scores = kmeans.predict(X_toy)
print('\nScores:', scores)
Linhas selecionadas como centros dos clusters: [18 1 19]
Centros selecionados:
0: [0.76864751 0.31399468]
1: [0.43840923 0.72346518]
2: [0.57262533 0.27604905]
Scores: [1 1 0 2 1 1 2 1 1 0 1 1 0 1 0 1 1 1 0 2]
plot_cluster(X_toy, scores, kmeans.cluster_centers_)
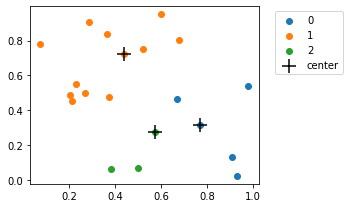
new_centroids = kmeans._update_centers(X_toy, verbose=True)
kmeans.cluster_centers_ = new_centroids
scores = kmeans.predict(X_toy)
print('\nScores:', scores)
Mudança dos centros:
0: [0.76864751 0.31399468] -> [0.85119693 0.29566242]
1: [0.43840923 0.72346518] -> [0.35510883 0.68531978]
2: [0.57262533 0.27604905] -> [0.48489564 0.13801218]
Scores: [1 1 0 2 1 1 2 1 1 0 1 1 0 1 0 1 1 1 0 2]
plot_cluster(X_toy, scores, kmeans.cluster_centers_)
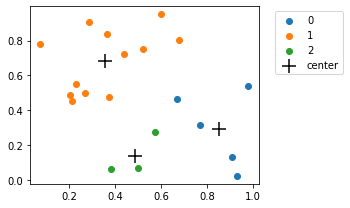
A inicialização faz toda a diferença. A literatura nos traz formas mais “espertas” de se inicializar os clusters. Por exemplo, esse artigo é uma boa referência no assunto e sua proposta é implementada no sklearn.
1.1.5. Estamos com o queijo, a faca, e a goiabada na mão para entender o nosso método fit.
Agora é só usar:
kmeans = KMeans(k=3)
kmeans.fit(X_toy, verbose=True)
Linhas selecionadas como centros dos clusters: [ 0 17 15]
Centros selecionados:
0: [0.07630829 0.77991879]
1: [0.36589039 0.83791799]
2: [0.20484909 0.49076589]
Mudança dos centros:
0: [0.07630829 0.77991879] -> [0.07630829 0.77991879]
1: [0.36589039 0.83791799] -> [0.55337517 0.78767871]
2: [0.20484909 0.49076589] -> [0.50183692 0.31854301]
Variação dos centros: 0.1555370227867891
Iteração 1
Mudança dos centros:
0: [0.07630829 0.77991879] -> [0.19990146 0.68219203]
1: [0.55337517 0.78767871] -> [0.5975801 0.76735957]
2: [0.50183692 0.31854301] -> [0.55868911 0.27832604]
Variação dos centros: 0.03204231220845901
Iteração 2
Mudança dos centros:
0: [0.19990146 0.68219203] -> [0.25246316 0.62451172]
1: [0.5975801 0.76735957] -> [0.64391805 0.75324789]
2: [0.55868911 0.27832604] -> [0.67609744 0.19340753]
Variação dos centros: 0.029431962695117678
Iteração 3
Mudança dos centros:
0: [0.25246316 0.62451172] -> [0.25246316 0.62451172]
1: [0.64391805 0.75324789] -> [0.64391805 0.75324789]
2: [0.67609744 0.19340753] -> [0.67609744 0.19340753]
Variação dos centros: 0.0
Variação dos centros é menor que "etol": 0.0. Parando.
<__main__.KMeans at 0x7fbd04936c70>
1.1.6. Tem algo misterioso faltando nesse código
E aquele parâmetro cycle_callback?
Eu deixei esse parâmetro sendo chamado em dois momentos:
- Quando novos centróides são definidos
- Quando eles são atualizados
cycle_callback é chamado como uma função… porque eu passarei uma função como parãmetro.
Ideia: vamos visualizar o que está acontecendo na nossa implementação, passo-a-passo. Para tal, vou aproveitar aquela função de plot que eu havia definido anteriormente.
def plot_callback_factory(delay=0.2):
# Recicla plots para simular animações
def plot_at_each_cycle(X, scores, centroids, fig=None, delay=delay):
if fig is not None:
fig.axes[0].clear()
# Chama a nossa função de plot
fig = plot_cluster(X, scores, centroids, fig)
# Exibe os resultados
fig.show()
fig.canvas.draw()
time.sleep(delay)
return fig
return plot_at_each_cycle
# Habilitarei plots interativos e desabilitarei a captura interativa dos plots
%matplotlib notebook
plt.ioff()
Resultado:
# Plots com delay de meio segundo entre atualizações
callback = plot_callback_factory(0.5)
kmeans = KMeans(k=3)
kmeans.fit(X_toy, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Voltaremos a esse tipo de plot novamente :D
1.2. (variante) k-Medians
Enquanto o k-Means utiliza a média dos pontos como protótipo dos clusters. Outra alternativa é utilizar a mediana como o “centro” de cada cluster. Isso tem o efeito de minimizar a norma Manhattan (1-norm), ao invés do quadrado da norma Euclidiana (2-norm), como no k-Means. Vamos aproveitar a nossa implementação do k-Means e mudar apenas o necessário:
class KMedians(KMeans):
def _clustering_criterion(self, X, center):
# Taxicab norm or Manhattan norm (1-norm)
return np.sum(np.abs(X - center), axis=1)
def _update_centers(self, X, verbose=False):
scores = self.predict(X)
new_centers = np.zeros_like(self.cluster_centers_)
for center_id in range(self.k):
# Aqui está a mudança!
new_centers[center_id] = np.median(X[scores == center_id], axis=0)
if verbose:
print('\nMudança dos centros:')
for center_id in range(self.k):
print(f'{center_id}: {self.cluster_centers_[center_id]} -> {new_center[center_id]}')
return new_centers
%matplotlib notebook
plt.ioff()
kmedians = KMedians(k=3, random_state=8)
kmedians.fit(X_toy, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
1.3 (variante) Partitioning Around Medoids (PAM) ou k-Medoids
O algoritmo PAM ou k-Medoids sempre utiliza pontos do próprio conjunto de dados como protótipo. Ele parte de um conjunto de medoids iniciais escolhidos aleatoriamente e funciona fazendo sucessivas substituições dos protótipos atuais por outros pontos que não são atualmente medoids, enquanto busca minimizar um função de distância. Aqui falamos diretamente em distância e, de fato, podemos usar qualquer métrica de distância com esse algorimo. Ao minimizar a distância total dos pontos para os medoids intuitivamente estamos escolhendo os “pontos mais centrais” nos clusters com os protótipos.
Um problema dessa abordagem de troca de medoids é o seu custo computacional.
class KMedoids(KMeans):
def __init__(self, k, etol=1e-3, max_iter=100, random_state=42, p=1.5):
super().__init__(k=k, etol=etol, max_iter=max_iter, random_state=random_state)
self.p = p
def _clustering_criterion(self, X, center):
# Estou utilizando a distância Minkowski
return np.sum((np.abs(X - center) ** self.p), axis=1) ** (1 / self.p)
def _update_centers(self, X, verbose=False):
best_cost = self._cost(X, self.cluster_centers_)
# Inicio com os centros atuais
new_centers = self.cluster_centers_.copy()
# Variavel auxiliar
aux_centers = self.cluster_centers_.copy()
for center_id in range(self.k):
# Aqui está a mudança!
for x in X:
# Se x já é medoid, pule
if np.all(np.isclose(aux_centers[center_id] - x, 0.)):
continue
aux_centers[center_id] = x
new_cost = self._cost(X, aux_centers)
if new_cost < best_cost:
best_cost = new_cost
new_centers[center_id] = x
else:
aux_centers[center_id] = new_centers[center_id]
if verbose:
print('\nMudança dos centros:')
for center_id in range(self.k):
print(f'{center_id}: {self.cluster_centers_[center_id]} -> {new_center[center_id]}')
return new_centers
def _cost(self, X, centers):
# Matriz com n_instances x n_clusters
errors = np.zeros((X.shape[0], self.k))
for center_id, center in enumerate(centers):
errors[:, center_id] = self._clustering_criterion(X, center)
selected = np.argmin(errors, axis=1)
return sum(sum(errors[selected == cluster_id, cluster_id]) for cluster_id in range(self.k))
%matplotlib notebook
plt.ioff()
kmedoids = KMedoids(k=3, random_state=8)
kmedoids.fit(X_toy, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
1.3. Explorando casos mais interessantes
Vou gerar alguns exemplos extras para observarmos como os algoritmos de agrupamento se comportam.
1.3.1 Blobs
from sklearn import datasets
# Estamos usando y apenas para Taxicab norm or Manhattan norm para propósitos educativos. Nosso problema é não supervisionado
X_blob1, y_blob1 = datasets.make_blobs(n_samples=100, centers=3, n_features=2, random_state=0, cluster_std=1)
plot_cluster(X_blob1, y_blob1)
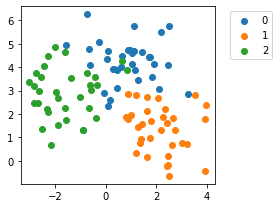
k-Means
%matplotlib notebook
plt.ioff()
# Note que "sabemos o número de clusters"
kmeans_blob1 = KMeans(k=3, random_state=8)
kmeans_blob1.fit(X_blob1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
k-Medians
%matplotlib notebook
plt.ioff()
# Note que "sabemos o número de clusters"
kmedians_blob1 = KMedians(k=3, random_state=8)
kmedians_blob1.fit(X_blob1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
k-Medoids
%matplotlib notebook
plt.ioff()
# Note que "sabemos o número de clusters"
kmedoids_blob1 = KMedoids(k=3, random_state=3)
kmedoids_blob1.fit(X_blob1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Vamos complicar um pouco as coisas
X_blob2, y_blob2 = datasets.make_blobs(n_samples=100, centers=4, n_features=2, random_state=0, cluster_std=0.5)
plot_cluster(X_blob2, y_blob2)
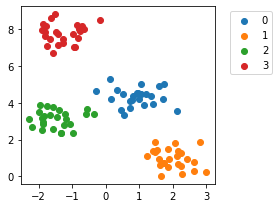
%matplotlib notebook
plt.ioff()
# Estou passando o número "errado" de clusters
kmeans_blob2 = KMeans(k=3, random_state=8)
kmeans_blob2.fit(X_blob2, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
O k-Means encontrará os três clusters, como pedimos. Ou quatro…
%matplotlib notebook
plt.ioff()
kmeans_blob2 = KMeans(k=4, random_state=8)
kmeans_blob2.fit(X_blob2, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Ou dez!
%matplotlib notebook
plt.ioff()
# Estou passando o número "errado" de clusters
kmeans_blob2 = KMeans(k=10, random_state=8)
kmeans_blob2.fit(X_blob2, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
1.3.2 Selecionando o número de clusters (referência)
Buscaremos avaliar as partições que encontramos utilizando métricas de avaliação.
1.3.2.1 Caso não-supervisionado: Elbow method
Foi o método apresentado em aula e é provavelmente uma das heurísticas mais conhecidas para a escolha do número de clusters no k-Means. Calculamos a soma das diferenças quadráticas de cada ponto para o centróide (within cluster sum of squares ou inertia) ao qual pertence e fazemos um plot variando o valor de k. Nesse gráfico procuramos pelo “ponto de cotovelo”. No sklearn ela pode ser acessada utilizando kmeans.inertia_, onde kmeans é um modelo já treinado.
A equação da Inertia (inércia) ou é dada por:
$\text{Inertia} = \sum_{c \in C} \sum_{x \in c} (x - \overline{c})^2$, onde $C$ é o conjunto de todos os clusters e $\overline{c}$ é o centróide do cluster $c$.
Nós a implementaremos aqui utilizando métodos do nosso modelo kmeans treinado. Se estiver utilizando o k-Means do sklearn substitua essa função pela propriedade inertia_ do KMeans.
def sum_inertia(X, kmeans):
scores = kmeans.predict(X)
sum_inertia = 0.
for cluster_id in np.unique(scores):
imask = scores == cluster_id
sum_inertia += np.sum(
kmeans._clustering_criterion(X[imask], kmeans.cluster_centers_[cluster_id]))
return sum_inertia
# Primeiro dataset
inertia_scores = []
for k in range(2, 10):
kmeans = KMeans(k=k, random_state=8)
kmeans.fit(X_blob1)
inertia_scores.append(sum_inertia(X_blob1, kmeans))
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(range(2, 10), inertia_scores)
ax.set_xlabel('k')
ax.set_ylabel('Inertia')
plt.show()
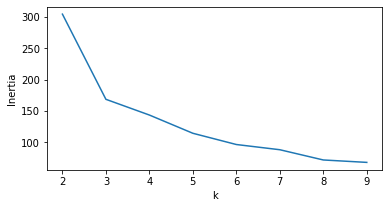
O “cotovelo” está em k=3, como esperado.
# Segundo dataset
inertia_scores = []
for k in range(2, 10):
kmeans = KMeans(k=k, random_state=8)
kmeans.fit(X_blob2)
inertia_scores.append(sum_inertia(X_blob2, kmeans))
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(range(2, 10), inertia_scores)
ax.set_xlabel('k')
ax.set_ylabel('Inertia')
plt.show()
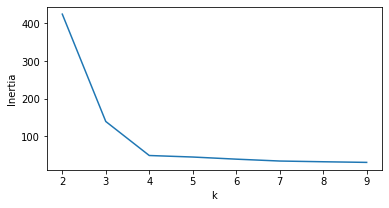
Aqui, a mudança mais brusca (cotovelo) ocorre em k=4.
1.3.2.2 Caso não supervisionado: silhueta (silhouette)
Uma forma simples de estimarmos o número de clusters é avaliarmos valores crescentes de k plotarmos os valores de silhueta obtidos. A nossa medida aqui é a silhueta que varia entre $[-1, 1]$, sendo $1$ o melhor valor possível. Essa métrica avalia a densidade das partições encontradas.
- Vantagens silhueta
- Métrica em intervalo bem definido: de -1 (ruim), passando por 0 (clusters com overlap), até 1 (bom)
- Os valores são altos quando os clusters são densos e bem separados, o que está intimamente ligado à noção usual de agrupamento.
- Desvantagem
- O k-Means cria estruturas convexas, de fato, estruturas similares à hiper-esferas (ou uma gaussiana multivariada). Essa métrica favorece esse tipo de estrutura. Clusters encontrados por outras estratégias de particionamento, como o agrupamento por densidade, tendem a obter menores valores de silhueta (e nem por isso são piores).
from sklearn.metrics import silhouette_score
# Primeiro dataset
silh_scores = []
for k in range(2, 10):
kmeans = KMeans(k=k, random_state=8)
kmeans.fit(X_blob1)
silh_scores.append(silhouette_score(X_blob1, kmeans.predict(X_blob1)))
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(range(2, 10), silh_scores)
ax.set_xlabel('k')
ax.set_ylabel('Silhouette')
plt.show()
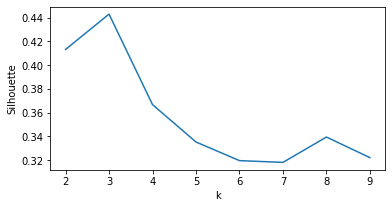
# Segundo dataset
silh_scores = []
for k in range(2, 10):
kmeans = KMeans(k=k, random_state=8)
kmeans.fit(X_blob2)
silh_scores.append(silhouette_score(X_blob2, kmeans.predict(X_blob2)))
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(range(2, 10), silh_scores)
ax.set_xlabel('k')
ax.set_ylabel('Silhouette')
plt.show()
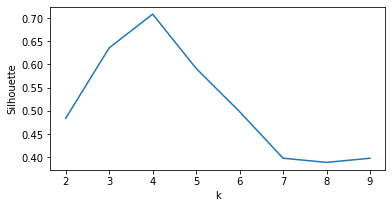
Escolhemos o ponto que maximiza a silhueta média (k=3 e k=4 para o primeiro e segundo casos, respectivamente).
Devemos lembrar que a silhueta é definida para cada ponto. Até agora consideramos apenas valores médios.
Abordagem mais geral
Utilizarei uma outra abordagem, sugerida pelo sklearn, baseada em silhouette analysis. Esta abordagem considera tanto a silhueta média, como a silhueta de cada ponto.
Definirei uma função de plot extra:
from sklearn.metrics import silhouette_score, silhouette_samples
import matplotlib.pyplot as plt
import matplotlib.cm as cm
def plot_silhouettes(X, k, random_state=42):
fig, ax = plt.subplots(figsize=(10, 5))
ax.set_xlim([-1, 1])
# Use esta linha para a implementação didática
clusterer = KMeans(k=k, random_state=random_state)
# Use essa linha se estiver usando a versão do sklearn
# clusterer = KMeans(n_clusters=k, random_state=random_state)
clusterer.fit(X)
cluster_labels = clusterer.predict(X)
# Silhueta para cada ponto
sample_silhouette_values = silhouette_samples(X, cluster_labels)
# Silhueta média
silhouette_avg = silhouette_score(X, cluster_labels)
y_lower = 10 # Padding
for i in range(k):
# Seleciona as silhuetas de cada cluster e as ordena
cluster_silh = sample_silhouette_values[cluster_labels == i]
cluster_silh.sort()
size_cluster = len(cluster_silh)
y_upper = y_lower + size_cluster
color = cm.nipy_spectral(float(i) / k)
ax.fill_betweenx(np.arange(y_lower, y_upper),
0, cluster_silh, facecolor=color,
edgecolor=color, alpha=0.7)
# Nome dos clusters
ax.text(-0.05, y_lower + 0.5 * size_cluster, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax.set_title(f'k={k}')
ax.set_xlabel('Silhueta')
ax.set_ylabel('Cluster')
# Linha vertical indicando a silhueta média
ax.axvline(x=silhouette_avg, color="red", linestyle="--")
ax.set_yticks([])
O que devemos observar nesse plot:
- O eixo x apresenta os valores de silhueta
- Os clusters são apresentados de forma separada
- Para cada cluster, as instâncias que a eles pertecem estão ordenadas pelos seus valores individuais de silhueta
- A silhueta média é indicada pela linha vertical (serrilhada) vermelha
Como escolher k a partir desse plot?
- Queremos que a largura das barras (variação no eixo
y) sejam similares. - Queremos que os comprimentos das barras estejam acima ou próximas do valor de silhueta médio (nunca abaixo).
- Queremos um valor de
kque não acarrete flutuações nos comprimentos (todas as barras com comprimentos similares). - Não queremos silhuetas negativas!
plot_silhouettes(X_blob2, 2, random_state=8)
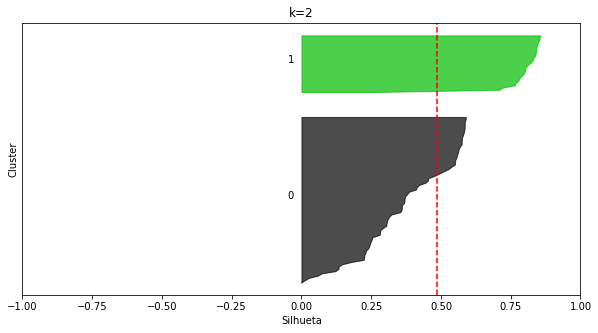
plot_silhouettes(X_blob2, 3, random_state=8)
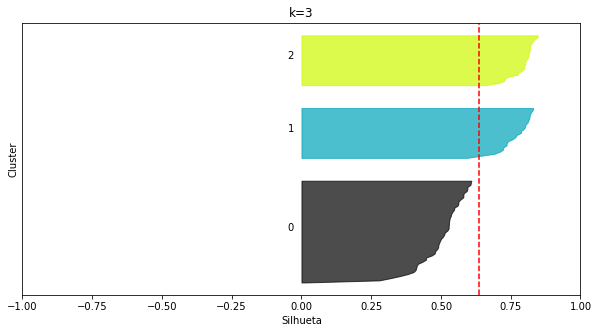
plot_silhouettes(X_blob2, 4, random_state=8)
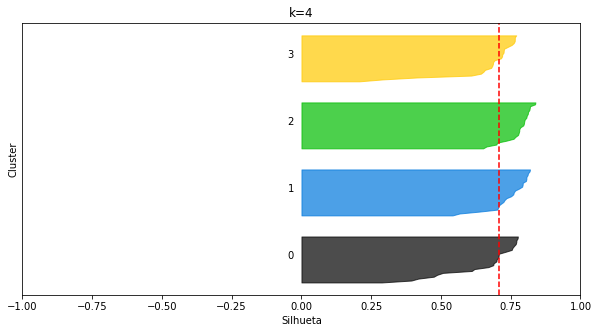
plot_silhouettes(X_blob2, 5, random_state=8)
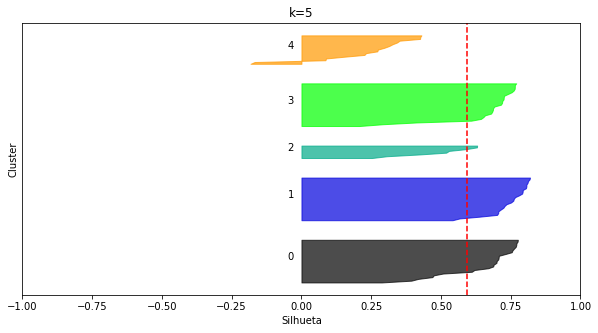
O nosso vencedor foi k=4, como esperado.
Atenção: notem como eu usei uma random seed diferente. Em nossa implementação, utilizamos apenas uma inicialização aleatória dos centroides. Como eu já mencionei, existem formas mais “espertas” de se fazer isso. Tais estratégias fazem toda a diferença! Além disso, o sklearn prevê também utilizar várias inicializações e escolher qual delas for a melhor (isso é um hiperparâmetro).
“Tarefa”: quem tiver curiosidade, experimente mudar os random_state nos gráficos anteriores e nos próximos para observar o impacto.
1.3.2.3 Caso supervisionado: Adjusted Rand Index
from sklearn.metrics import adjusted_rand_score
# Primeiro dataset
rand_scores = []
for k in range(2, 10):
kmeans = KMeans(k=k, random_state=8)
kmeans.fit(X_blob1)
rand_scores.append(adjusted_rand_score(y_blob1, kmeans.predict(X_blob1)))
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(range(2, 10), rand_scores)
ax.set_xlabel('k')
ax.set_ylabel('Adjusted Rand Index')
plt.show()
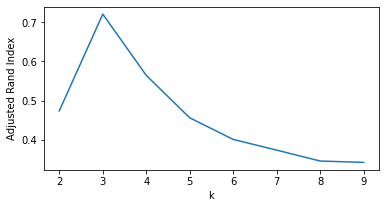
# Segundo dataset
rand_scores = []
for k in range(2, 10):
kmeans = KMeans(k=k, random_state=8)
kmeans.fit(X_blob2)
rand_scores.append(adjusted_rand_score(y_blob2, kmeans.predict(X_blob2)))
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(range(2, 10), rand_scores)
ax.set_xlabel('k')
ax.set_ylabel('Adjusted Rand Index')
plt.show()
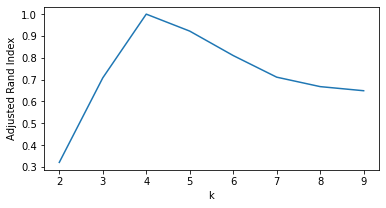
Vantagens do Adjusted Rand Index (ARI):
- Predição aleatória origina um valor de ARI próximo de zero
- Ranges bem definidos: $[-1, 1]$
- $-1$ é ruim
- $0$ é a predição aleatória
- $1$ é o melhor valor possível
- Ignora permutações
- É simétrica
ARI(A, B) == ARI(B, A) - Não assume nada sobre a estrutura dos clusters
Desvantagem:
- Supervisionada, o que não é realístico na maioria dos casos
1.3.3. Nem tudo são flores: dataset Circles
X_circ1, y_circ1 = datasets.make_circles(n_samples=500, noise=0.05, random_state=8, factor=0.1)
plot_cluster(X_circ1, y_circ1)
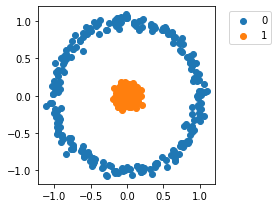
Dois clusters! Sopinha de algodão, certo? Vamos ver
%matplotlib notebook
plt.ioff()
kmeans_circ1 = KMeans(k=2, random_state=8)
kmeans_circ1.fit(X_circ1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
kmeans_circ1 = KMeans(k=2, random_state=1)
kmeans_circ1.fit(X_circ1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
kmeans_circ1 = KMeans(k=2, random_state=3)
kmeans_circ1.fit(X_circ1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
E agora? Uma saída poderia ser aumentar o número de clusters e contar com um especialista humano para nos dizer que múltiplos grupos representam um mesmo conceito:
%matplotlib notebook
plt.ioff()
kmeans_circ1 = KMeans(k=5, random_state=8)
kmeans_circ1.fit(X_circ1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Nesse caso, e para essa seed aleatória (e apenas uma inicialização) temos que os clusters $k \in {0, 2, 3, 4}$ representam o mesmo “conceito”, i.e., o círculo externo. Nós sabemos isso porque nossos dados estão em duas dimensões e foram gerados artificialmente.
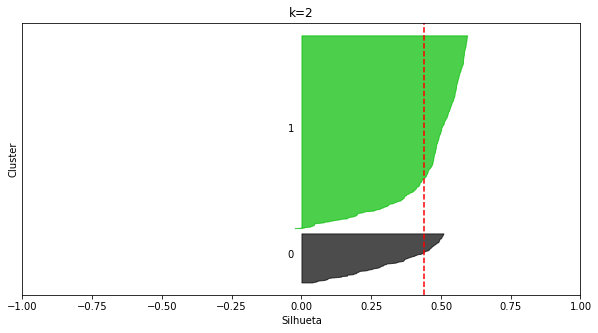
plot_silhouettes(X_circ1, 2, random_state=8)
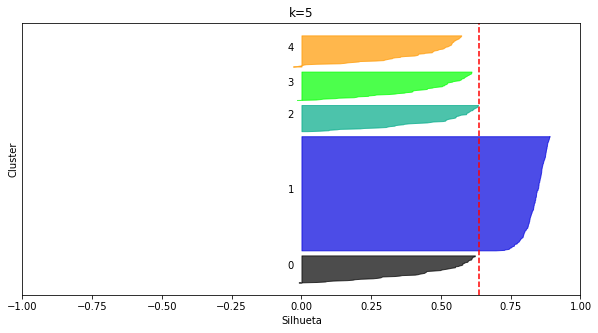
plot_silhouettes(X_circ1, 5, random_state=8)
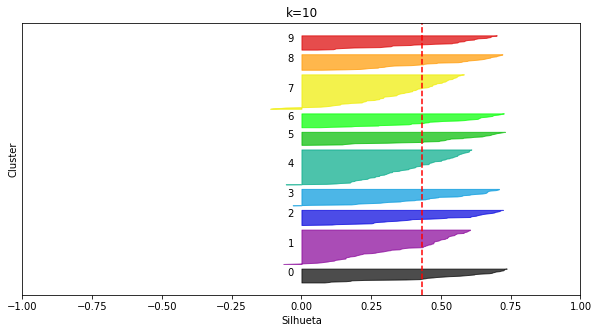
plot_silhouettes(X_circ1, 10, random_state=8)
%matplotlib notebook
plt.ioff()
kmeans_circ1 = KMeans(k=10, random_state=8)
kmeans_circ1.fit(X_circ1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Percebemos que apesar de k=5 responder bem ao nosso problema, como observado empiricamente, a silhueta está privilegiando estruturas (hiper-esféricas) circulares e densas, como previamente discutido. Por essa razão $k=10$ poderia ser uma escolha boa segundo os critérios previamente discutidos.
O problema vai mais longe… E se a estrutura fosse mais dúbia?
X_circ2, y_circ2 = datasets.make_circles(n_samples=500, noise=0.05, random_state=8, factor=0.7)
plot_cluster(X_circ2, y_circ2)

%matplotlib notebook
plt.ioff()
# k-Means
kmeans_circ2 = KMeans(k=5, random_state=8)
kmeans_circ2.fit(X_circ2, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
# k-Medians
kmedians_circ2 = KMedians(k=5, random_state=8)
kmedians_circ2.fit(X_circ2, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
É, agora complicou o meio de campo. :P
E esse é apenas um dos exemplos. Podemos manter o padrão da primeira variante desse dataset com a adição de ruído para perceber um outro problema nesse tipo de abordagem.
X_circ3, y_circ3 = datasets.make_circles(n_samples=500, noise=0.15, random_state=8, factor=0.3)
# Vou até acelerar os plots:
callback = plot_callback_factory(0.1)
plot_cluster(X_circ3, y_circ3)

%matplotlib notebook
plt.ioff()
# k-Means
kmeans_circ3 = KMeans(k=2, random_state=8)
kmeans_circ3.fit(X_circ3, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
# k-Means
kmeans_circ3 = KMeans(k=3, random_state=8)
kmeans_circ3.fit(X_circ3, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
# k-Means
kmeans_circ3 = KMeans(k=5, random_state=8)
kmeans_circ3.fit(X_circ3, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
# k-Means
kmeans_circ3 = KMeans(k=10, random_state=8)
kmeans_circ3.fit(X_circ3, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
1.3.4 Moons
X_moons1, y_moons1 = datasets.make_moons(random_state=8, noise=0.05)
plot_cluster(X_moons1, y_moons1)

%matplotlib notebook
plt.ioff()
# k-Means
kmeans_moons1 = KMeans(k=2, random_state=8)
kmeans_moons1.fit(X_moons1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
# k-Means
kmeans_moons1 = KMeans(k=5, random_state=8)
kmeans_moons1.fit(X_moons1, cycle_callback=callback)
%matplotlib inline
<IPython.core.display.Javascript object>
plot_silhouettes(X_moons1, 2, random_state=8)
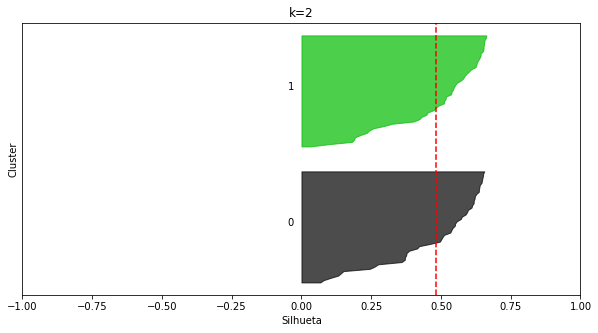
kmeans_moons1 = KMeans(k=2, random_state=8)
kmeans_moons1.fit(X_moons1)
adjusted_rand_score(y_moons1, kmeans_moons1.predict(X_moons1))
0.26295510204081635
plot_silhouettes(X_moons1, 3, random_state=8)
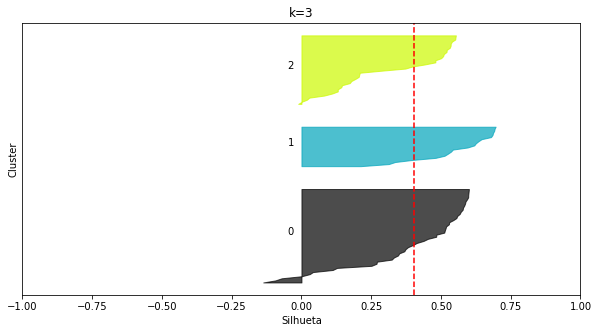
kmeans_moons1 = KMeans(k=3, random_state=8)
kmeans_moons1.fit(X_moons1)
adjusted_rand_score(y_moons1, kmeans_moons1.predict(X_moons1))
0.2706764455503896
plot_silhouettes(X_moons1, 5, random_state=8)
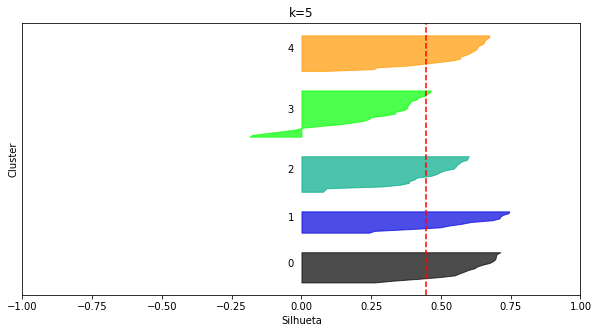
kmeans_moons1 = KMeans(k=5, random_state=8)
kmeans_moons1.fit(X_moons1)
adjusted_rand_score(y_moons1, kmeans_moons1.predict(X_moons1))
0.2683287347260544
Houston we have a problem!
O víes de aprendizado dos algorítmos baseados em protótipos não é adequado para esses problemas cujos clusters não são convexos e nem hiper-esféricos. De fato, o k-Means pode ser visto como um caso especial de Gaussian Mixture models. Se abstrairmos um pouco, o que estamos fazendo é posicionar funções gaussianas multivariadas nos dados. A média dessas gaussianas é justamente os centróides. Cool, huh?
Avaliaremos um outro tipo de agrupamento particional para tentar resolver esse problema específico.
Mas calma! Não é o fim da linha para o nosso amigo k-Means. Deixo aqui esse post que achei muito interessante. O autor demonstra como podemos combinar agrupamento hierárquico (a ser ainda discutido) com o k-Means para lidar com problemas não-convexos.
2. Clustering particional: densidade
Density-based spatial clustering of applications with noise (DBSCAN) é um algoritmo para agrupamento de dados que funciona de forma diferente das abordagens que vimos até agora. O DBSCAN não assume nada sobre as estruturas dos clusters nos dados. De fato, para o DBSCAN, clusters são regiões de alta densidade separadas por regiões de baixa densidade, não importando a sua forma. Além disso, prevê a existência de pontos que não pertencem a nenhum dos clusters, em outras palavras, outliers.
O DBSCAN parte dos seguintes pressupostos principais:
- Core points: são pontos em regiões de alta densidade;
- Border points: pontos “acessíveis” através de um core point, mas que não são core points.
- Noise/Outlier: pontos que não são acessíveis por um ponto core.
O DBSCAN possui dois hiper-parâmetros:
eps: define um raio de vizinhança, em outras palavras, um ponto $p$ está conectado a outro ponto $q$ se $d(p, q) \le \epsilon$, onde $d$ é uma função de distância (aqui não assumimos nada sobre a métrica de distância utilizada).min_samples: define quantos pontos devem estar naeps-vizinhança de um ponto, para que tal ponto seja considerado core.
No entanto, o DBSCAN tem problemas com datasets que possuem muitas variações em densidade e são esparsos. Se os clusters possuem diferentes densidades não será possível se encontrar uma boa combinação de eps e min_samples.
from sklearn.neighbors import KDTree
class DBSCAN:
def __init__(self, eps=0.5, min_samples=4, p=2):
self.eps = eps
self.min_samples = min_samples
self.p = p # Distância Minkowski
def _minkowski_distance(self, x1, x2):
return np.sum(np.abs(x1 - x2) ** self.p, axis=1) ** (1 / self.p)
def fit(self, X, cycle_callback=None):
# Plot inicial vazio
p_out = None
# Indices na base dados
indices = np.array(range(X.shape[0]))
# O label de todos os pontos é indefinido
self.labels_ = np.full(X.shape[0], -999)
# Faz primeiro plot
if cycle_callback is not None:
p_out = cycle_callback(X, self.labels_, fig=p_out)
# Core samples
self.core_sample_indices_ = set()
# Estrutura para buscar vizinhos mais próximos
kdtree = KDTree(X, p=self.p)
c = 0 # Id do cluster
for i in range(X.shape[0]):
# Já é core point, ponto de borda ou outlier
if self.labels_[i] != -999:
continue
# Todos os vizinhos de X_i, com ele incluso no raio eps
neighbors = kdtree.query_radius(X[i].reshape(1, -1), r=self.eps)[0]
if len(neighbors) < self.min_samples: # Não é denso o suficiente
self.labels_[i] = -1 # Noise ou outlier
# Atualiza plot
if cycle_callback is not None:
p_out = cycle_callback(X, self.labels_, fig=p_out)
continue
self.core_sample_indices_.add(i)
self.labels_[i] = c
# Atualiza plot
if cycle_callback is not None:
p_out = cycle_callback(X, self.labels_, fig=p_out)
# Remove X_i de sua própria vizinhança e define conjunto para expansão
seed_set = neighbors[neighbors != i].tolist()
# Agora expandiremos a vizinhança do nosso ponto p
for j in seed_set:
if self.labels_[j] == -1: # É ruido (até agora)
self.labels_[j] = c # Muda ponto previamente considerado ruído
# Atualiza plot
if cycle_callback is not None:
p_out = cycle_callback(X, self.labels_, fig=p_out)
if self.labels_[j] != -999:
continue # Ponto já foi processado
self.labels_[j] = c
# Atualiza plot
if cycle_callback is not None:
p_out = cycle_callback(X, self.labels_, fig=p_out)
# Vamos procurar mais pontos que podem ser acessados por esse elemento
# conectado ao nosso core point
neighbors = kdtree.query_radius(X[j].reshape(1, -1), r=self.eps)[0]
if len(neighbors) >= self.min_samples: # Também é um core point
seed_set.extend(neighbors.tolist()) # Adiciona pontos para o seed set
self.core_sample_indices_.add(j)
c += 1 # Vamos para o próximo cluster!
# Converte para array do numpy (só para ficar parecido com o sklearn)
self.core_sample_indices_ = np.array(list(self.core_sample_indices_))
# Vou salvar os core points (só para ficar igual ao sklearn também)
self.components_ = np.zeros((len(self.core_sample_indices_), X.shape[1]))
for i, core_p in enumerate(self.core_sample_indices_):
self.components_[i] = X[core_p]
return self
def fit_predict(self, X):
self.fit(X)
return self.labels_
Criarei um função diferente para plot, visto as diferenças do algoritmo de clustering
def dbscan_plot_callback_factory(delay=0.2):
# Recicla plots para simular animações
def plot_at_each_cycle(X, labels, fig=None, delay=delay):
if fig is not None:
fig.axes[0].clear()
ax = fig.axes[0]
else:
fig, ax = plt.subplots(figsize=(5, 3))
label_transformer = lambda x: (f'Cluster {x}' if x >= 0 else 'Noise') \
if x >= -1 else 'Indefinido'
marker_transformer = lambda x: ('o' if x >= 0 else 'x') if x >= -1 else '.'
# Transforma cluster label em valor que pode mapeado (estou supondo no max 15 clusters)
c_normalizer = matplotlib.colors.Normalize(vmin=0., vmax=15)
cmap = matplotlib.cm.get_cmap('hsv')
color_transformer = lambda x: ((.5, .5, .5, 1.) if x == -999 else (0., 0., 0., 1.)) \
if x < 0 else cmap(c_normalizer(x))
for label in np.unique(labels):
imask = labels == label
colors = [color_transformer(label) for _ in range(np.sum(imask))]
ax.scatter(X[imask, 0], X[imask, 1], label=label_transformer(label),
marker=marker_transformer(label), c=colors)
ax.legend(loc='upper left', bbox_to_anchor=(1.05, 1))
plt.tight_layout()
plt.close()
# Exibe os resultados
fig.show()
fig.canvas.draw()
time.sleep(delay)
return fig
return plot_at_each_cycle
Função callback para plot
dbscan_callback = dbscan_plot_callback_factory(0.2)
DBSCAN com valores default
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN()
dbscan.fit(X_toy, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Não deu muito certo. Precisamos ter em mente características dos nossos dados (notem que os ranges dessa base são entre 0 e 1). Vamos tentar outros valores:
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN(eps=0.2)
dbscan.fit(X_toy, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Que tal esses?
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN(eps=0.25)
dbscan.fit(X_toy, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Dataset blob
dbscan_callback = dbscan_plot_callback_factory(0.)
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN()
dbscan.fit(X_blob1, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Let’s try again
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN(min_samples=3)
dbscan.fit(X_blob1, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Vamos tentar a outra variação que criamos para esse dataset
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN()
dbscan.fit(X_blob2, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
Está melhor.
Vamos supor que nesse dataset nós esperaramos encontrar quatro grupos (sabemos as características do problema) e estamos percebendo muitos ruídos. Podemos tentar aumentar o valor de eps:
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN(eps=0.7)
dbscan.fit(X_blob2, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
A escolha de hiperparâmetros parece uma tarefa um pouco mais complicada nesse caso (e ainda temos o auxilio das visualizações). Escolher o k do k-Means foi muito mais fácil nesses casos!
2.1 Usando o DBSCAN em geometrias não-convexas
Como será que o DBSCAN se sai nos casos onde o k-Means teve suas dificuldades?
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN()
dbscan.fit(X_circ1, cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
%matplotlib notebook
plt.ioff()
dbscan = DBSCAN(eps=0.15, p=1, min_samples=6)
dbscan.fit(X_circ2, cycle_callback=dbscan_callback)
%matplotlib inline
(variei muito os hiperparâmetros até chegar nisso)
%matplotlib notebook
plt.ioff()
from sklearn.preprocessing import StandardScaler
dbscan = DBSCAN()
dbscan.fit(StandardScaler().fit_transform(X_moons1), cycle_callback=dbscan_callback)
%matplotlib inline
<IPython.core.display.Javascript object>
No fim das contas, tudo é uma questão de boas escolhas :D
2.2 Como escolher os valores de eps e min_samples
Essa não é uma resposta trivial. Recentemente, os autores do algoritmo publicaram um artigo revisitando vários pontos do DBSCAN e discutem algumas possíveis formas de se escolher os seus parâmetros.
min_samples: uma “thumb rule” para selecionar esse hiper-parâmetro é2 * n_features. Notem que o valor padrão é4e estamos utilizando exemplos bi-dimensionais. No entanto, para datasets muito grandes, com muitas features, ou com muito ruído, é uma boa ideia mudar os valores desse parâmetro.eps: esse hiper-parâmetro é mais complicado de ser ajustado e também depende da função de distância utilizada. Idealmente ele deve ser o menor possível e deveria ser ajustado com base em um especialista do domínio. Por exemplo, se estamos agrupando dados de GPS, um especialista poderia nos dizer que a distância de 1km deveria ligar dois pontos. Nesse caso, pode ser válido ajustar também o valore demin_samples. Os autores do DBSCAN aconselham deixar um dos hiper-parâmetros livres. Existem heurísticas parecidas com a do “cotovelo”, mas não são tão triviais como no caso do k-Means.
Em geral, ao explorarmos valores de hiper-parâmetros:
Não queremos que muitos pontos sejam marcados como ruído:
- Os autores do DBSCAN afirmam que um valor adequado de instâncias identificadas como ruído está entre $1%$ e $30%$
Se o maior componente (cluster) tem muitos dados (entre $20%$ até $50%$), isso pode ser um indício de que o valor de
epsescolhido está muito alto. Nesse caso, os autores apontam dois caminhos:- Diminuir o valor de
eps - Utilizar uma abordagem modificada do DBSCAN que utilizam hierarquias: OPTICS e HDBSCAN. Ambos esses algoritmos estão disponíveis no
sklearn.
- Diminuir o valor de
De fato, a seção de clustering do sklearn apresenta vários algoritmos de agrupamento que estão disponíveis, assim como métricas de avaliação, dicas e comparações entre os clusterizadores. Existe, inclusive, uma tabela comparativa dos algorítmos disponíveis apontando casos de uso. Recomendo também a seção 4 do artigo que mencionei anteriormente, dos próprios autores do DBSCAN.
3. Relembrando as diferenças
Protótipos vs Densidade
- O k-Means e similares utilizam uma noção de um centro, ou ponto representativo do grupo
- O DBSCAN não possui tais noções. Os pontos core não definem um protótipo para o grupo: um mesmo cluster pode possuir vários pontos core.
Número de clusters
- O número é pré-definido no k-Means
- Porém existem várias estratégias para se encontrar valores adequados de k
- Os grupos encontrados são hiper-esféricos
- O número é encontrado automaticamente no DBSCAN
- No entanto, encontrar valores para o seus hiper-parâmetros não é trivial
- Nada é assumido acerca da forma dos grupos
- O número é pré-definido no k-Means
Ruídos e outliers
- O k-Means é sensível a ruídos e outliers (esses tipo de dados podem deslocar os centros)
- O DBSCAN prevê a existência de ruídos nos dados (o algorítmo deve estar bem ajustado para que funcione bem)
Inicialização
- O resultado do k-Means depende de sua inicialização
- O DBSCAN é determinístico
Para uso em emergências:
Executa as porções essenciais do código caso algum problema ocorra. Evita que seja necessário rodar todas as animações sequencialmente.
%%javascript
Jupyter.notebook.execute_cells([0, 3, 4, 5, 7, 37, 40, 44, 47, 50, 58, 65, 73, 78, 86,
92, 105, 109, 115, 126, 128, 138])